来源公众号:隔岸村 作者:深圳知青
每次考试之后,教师不仅要进行成绩分析,还要对命题质量进行分析。比如,成绩是不是呈现正态分布?试卷的难度是过于简单还是偏难?区分度是否合理?
教师最关心的平均问题。
我们知道,考试成绩的分布最好是正态分布,当难度为0.5时,正态分布的图形最好,区分度也相对好。但是这样一来,必然有一半的学生不及格。难度到底该多少,既能让成绩呈现正态分布,又能让大多数同学及格?
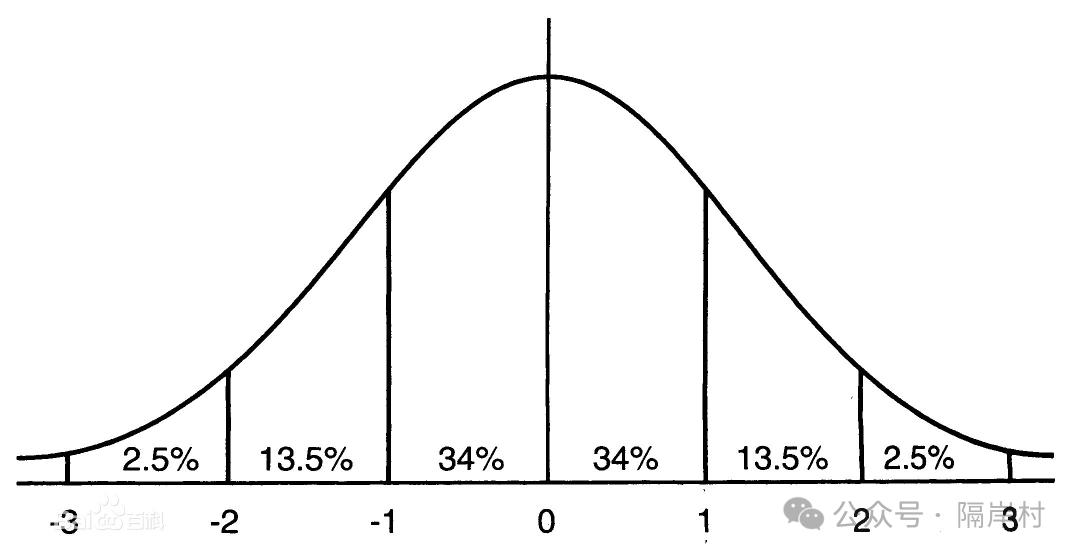
标准的正态分布下,分数分布要求是:平均分上下一个标准差的差距的人数分别占比34%,两个标准差差距的人数分别占比13.5%,三个标准差差距的人数分别占2.5%。如下图:
根据湖南省教育考试院的数据,我们可以观察到2023年高考分数的分布情况。假设某一科目的满分为150分,平均分为100分,标准差为15分。在这种情况下,大约68%的考生分数会落在85分到115分之间,而95%的考生分数则会落在70分到130分之间。这种数据分布不仅能够帮助我们理解考生的表现,还能为学校的教学调整提供参考。
通过分析高考分数的正态分布,我们可以更好地理解各个分数段的考生所占比例。例如,分数在115分以上的考生仅占总人数的16%,而在85分以下的考生也大约占16%。这样的分布情况不仅让家长和学生们对自己的成绩有了更清晰的定位,也为学校的教学质量评价提供了依据。
来源https://www.sohu.com/a/908877963_121956425
假定一个班有50个学生,平均分为72分,标准差为8,那么,理想状态下,64-72分和72-80分的学生应分别为17人,56-64分和80-88分的人数应分别7人,以此类推。
这只是理想状况。我们知道,正态分布分为正态分布、正偏态和负偏态三种。一次难度适中信度可靠的考试,学生的成绩若接近正态分布,反映中等成绩的考生居多,峰值偏左则为正 偏态分布,反映低分的学生居多,峰值偏右则为负偏态分布,反映高分的学生居多。
(一)偏度
如何计算一次考试的成绩呈现正偏态或者负偏态呢?是不是需要用分数段示意图去观察呢?很明显,用示意图观察不会非常精确。如何精准评价其偏态的状态呢?EXECL里有个专门的函数SKEW。
偏斜度表明分布相对于平均值的不对称程度。 正偏斜度表明分布的不对称尾部趋向于更多正值。 负偏斜度表明分布的不对称尾部趋向于更多负值。
语法:
SKEW(number1, [number2], …)
SKEW 函数语法具有下列参数:
number1, number2, … Number1 是必需的,后续数字是可选的。 用于计算偏斜度的 1 到 255 个参数。 也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
如前文所列的成绩,其偏态值为-3,表明成绩呈现严重的负偏态。计算结果见下图:
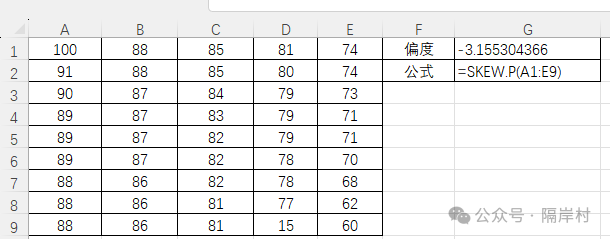
偏态值为多少合适呢?一般来说偏态值在- 1到+1 的范围之内就可以认为成绩基本呈正态分布。 偏度为0,表示该总体数据分布形态与正态分布的偏斜程度相同;偏度大于0,表示该总体数据分布形态与正态分布相比正偏或右偏,即有一条长尾巴拖在右边,数据右端有较多的极端值;偏度小于0,表示该总体数据分布形态与正态分布相比为负偏或左偏,即有一条长尾拖在左边,数据左端有较多的极端值。偏度的绝对值数值越大,表示其分布形态的偏斜程度越大。
(二)峰度
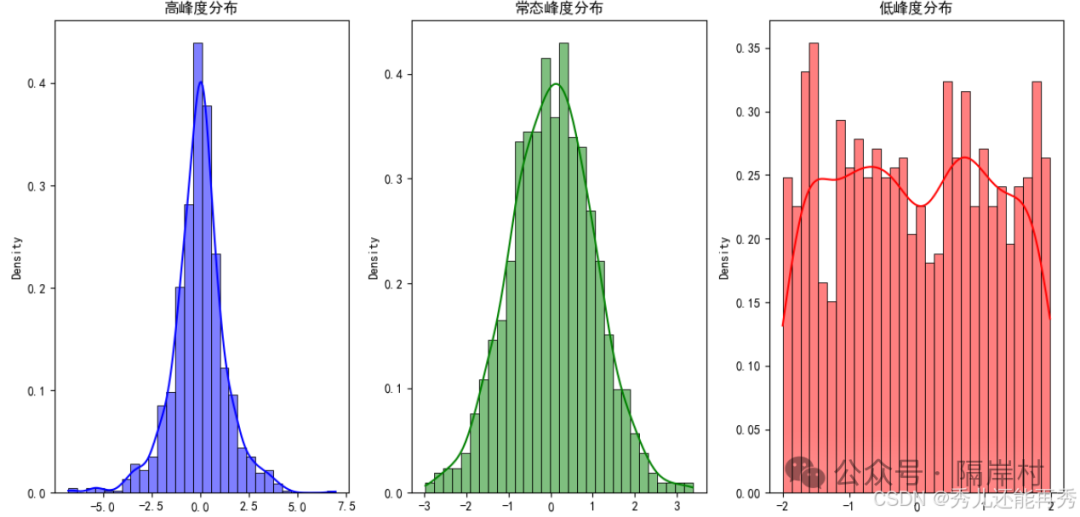
衡量数据分布的尖锐程度或尾部的厚度。
高峰度:分布曲线尖锐,尾部较重,峰度较高,表示更多极值。
常态峰度:类似正态分布,峰度接近零。
如下图:
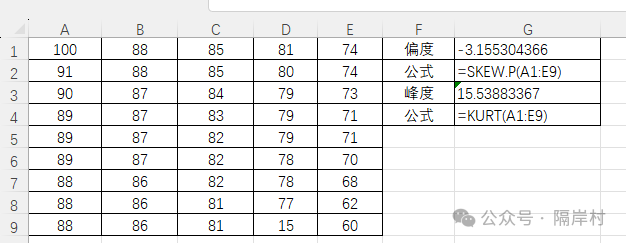
使用函数 KURT (data_range) 计算峰度。 正态分布的峰度为3,Excel计算的峰度通常为减3后的值,因此正态分布的峰度在Excel中应接近0。 偏度和峰度接近0,可以初步认为数据符合正态分布。
前例中成绩的峰度计算结果见下图:
正态分布的偏度和峰度的应用可参见迮燕华的文章《正态分布在高校成绩分析中的应用》:
1.偏度>0,峰度>0。该成绩分布形态与正态分布相比右偏且较为陡峭,在低分段过于集中。原因可能有试题较难;老师存在提分现象等等。
2.偏度>0,峰度<0。该成绩数据分布形态与正态分布相比右偏且较为平坦,即在低分段分布较为平坦。出现这种情况,可能的原因有试题过难;学生的整体学习效果较差,且学习水平不一,处于中游的学生不多。
3.偏度<0,峰度>0。该成绩数据分布形态与正态分布相比左偏且较为陡峭,即在高分段过于集中。可能的原因有试题过于简单,难点少;学生的整体学习效果较好等等。
4.偏度<0,峰度<0。该成绩数据分布形态与正态分布相比左偏且较为平坦,即在高分段分布较为平坦。出现这种情况,可能的原因有试题过于简单;学生的整体学习效果较好,学习水平不一,处于中游的学生不多。
所以,考试成绩出来之后,我们要分析成绩的正态分布情况,及时调整教学策略。



 扫码安装网站APP(Android版)
扫码安装网站APP(Android版)


近期评论