命题研究 | 还原2025年广东卷16题的命制过程

 

来源公众号：梧桐之生　作者：梧桐老师

后台有读者对广东卷16题命题素材的来源感兴趣，梧桐老师此前已经对16题的出题背景写过一篇分析，这篇推文就给大家溯源并尝试还原一下试题是怎么命制的。结合16题给出的数据来看，情境是来自于gnomAD数据库(目前公认的最大、最常用的人群基因频率数据库)提供的demo数据，这个数据库针对“预测一组变异对是顺式还是反式的”写了一篇详细的介绍。梧桐老师结合原介绍及自己的理解写下这篇推文。

研究背景

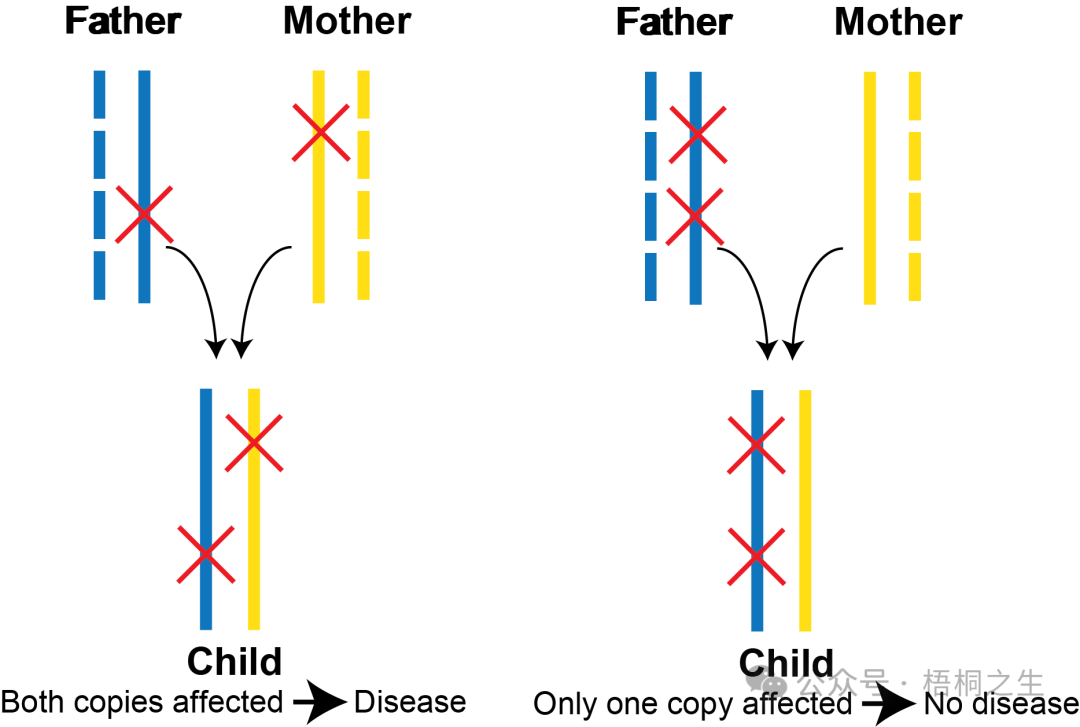
一个基因中的一对变异可呈顺式（发生在基因的同一条拷贝）或反式（发生在基因的不同拷贝）分布，这些变异可能对基因功能产生破坏性影响（如功能缺失），也可能呈中性。区分顺式和反式分布，对于解读变异引发常染色体隐性疾病的风险至关重要——此类疾病的发生需满足两个条件：1、基因的两条拷贝均携带变异（即呈反式分布）（下图左侧情况）2、变异会破坏基因功能。

(梧桐老师注：针对反式变异引发常染色体隐性遗传病这一问题，2024年河北卷出过一道很漂亮的题，不理解的读者可以先做完此题再来看这篇推文)

在上图中两组示例家系父母及子代中，父亲传递给子代的基因拷贝链以蓝色实线标注，母亲传递的基因拷贝链以黄色实线标注。左侧家系中，子代分别从父亲和母亲处各继承一个致病性变异，由于基因的两条拷贝链均携带致病性变异，因此该子代存在患隐性疾病的风险；右侧家系中，子代的两个变异均遗传自父亲，仅基因的一条拷贝链携带变异，不足以引发隐性疾病。

然而，在使用短读长(short reads)的第二代测序技术的绝大多数场景中，仅通过子代的DNA测序结果，无法区分上述两种情况。这是因为大多数变异对之间的距离超过了单条测序读长的长度，因此无法仅凭子代的测序数据确定其单倍型定相。为解决这一问题，临床遗传学家通常会对父母的DNA进行测序：若两个变异呈顺式分布，则它们应同时存在于父母中的一方；若呈反式分布，则两个变异分别存在于父母双方。但对父母DNA进行测序会增加成本，且父母的DNA样本并非总能获取。有时，研究人员可通过长读长测序技术辅助推断单倍型定相，但该技术目前成本仍较高。

目前已有多种准确高效的算法可用于确定人群中常见变异的单倍型定相，但对于罕见变异（这类变异通常在孟德尔疾病中具有重要意义），单倍型定相并非易事。此外，外显子测序数据仅覆盖基因组的极小部分，无法提供足够密度的周边变异信息以实现精准的单倍型定相；同时，单倍型定相分析计算量大，技术难度较高；最后，该分析需完整的变异数据（即超出临床遗传学报告所提供的信息范围），而终端用户往往无法获取这些完整数据。

研究方法

为应对上述挑战，gnomAD开发一种全新的单倍型定相方法：利用变异间的遗传关联（连锁情况）在人群个体中具有共享性这一特征。也就是说，如果某两个变异在人群多数个体中呈顺式分布，则它们在特定个体的DNA中也大概率呈顺式分布；同理，若某两个变异在人群中其他个体中呈反式分布，则它们在特定个体的DNA中最可能是呈反式分布。
然而，这种遗传关联仅会因以下两种机制被打破：

1.两个变异位点间的重组。但若变异在物理位置上距离较近（基因内的大多数变异均符合这一特征），则重组率会较低。

2.复发性突变(Recurrent mutation)。若某变异在人群进化事件中独立发生多次，则变异间的遗传关联会失去可靠性。

基于“单倍型相位(连锁状况)在人群个体中是共享的”这一特征，若能确定gnomAD数据库中变异对的单倍型相位，便可帮助用户预测特定样本中变异对的遗传关联情况。

对多种适用于gnomAD数据库变异定相的算法进行了测试，最终选择了期望最大化（E-M）算法。该算法的定相结果准确、计算量可控且易于解读。其核心逻辑为：若某一对变异在人群中多个个体中频繁或始终同时出现（即共现），则它们可能位于同一条单倍型上；反之，若这对变异在人群中个体中极少或从未同时出现，则它们可能位于不同的单倍型上。

随后，对gnomAD数据库中每个基因内符合特定要求的所有变异对进行了定相分析，并在三联体家系数据中进行了验证，结果显示不同人群的定向结果准确率基本超过90%。（梧桐老师注:三联体家系同时含父母与子代，这类样本的真实相位是已知的，更具体的测试结果请参考原文）

以PCSK9基因为例，介绍使用方法

（梧桐老师注：gnomAD数据库在介绍变异对定相的使用方法时，使用的demo是来自PCSK9基因的一对变异，这个示例数据最终被用于广东卷16题的命制）

首先，在页面输入变异对的信息：

理论上，这对变异可以是顺式，也可以是反式的：

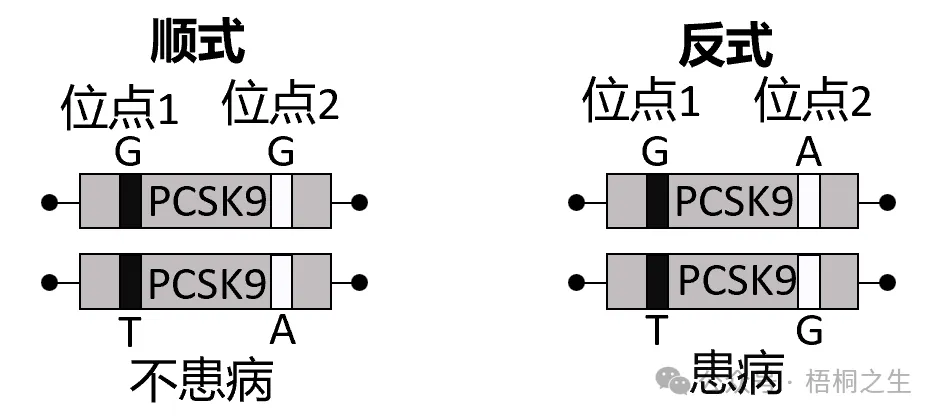
提交后，gnomAD会查询后台的数据记录，并返回一个按大陆人群祖先划分的表格：对于每个祖先人群，表格列出了 gnomAD 数据库中该人群中，与 “两个变异位于不同单倍型（反式，trans）” 相符的样本数量，以及与 “两个变异位于同一单倍型（顺式，cis）” 相符的样本数量。

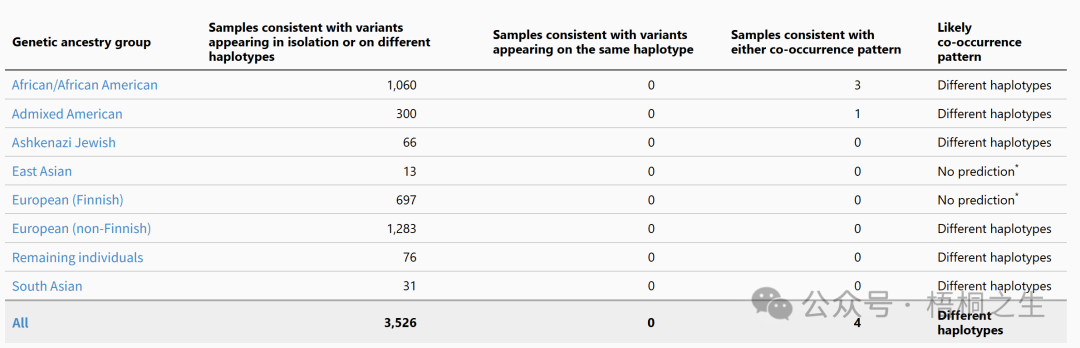
例如，上表非洲人群中有1060个样本是反式的，0个样本是顺式的，3个样本无法确定顺反。

将上表中所有人群的相位汇总，按照包含目标变异对的 9 种可能基因型的表格展开，就可以得到下面这个3×3矩阵（梧桐老师注：这个矩阵内的数据就是16题的数据来源，所以原题中的“某人群”实际上是表格中8个人群数据的汇总）：

矩阵中，红色代表变异对是反式的，即位于不同单倍型上；蓝色代表变异对是顺式的，即位于同一单倍型上，紫色代表变异对不确定顺式还是反式。注意，这个矩阵是人群中9种基因型组合的统计结果。接下来，数据库会基于这个数据利用EM算法进行推测，最终给出一个该人群中单倍型的估算结果：

上面这个估算结果，翻译一下就是长这个样子:

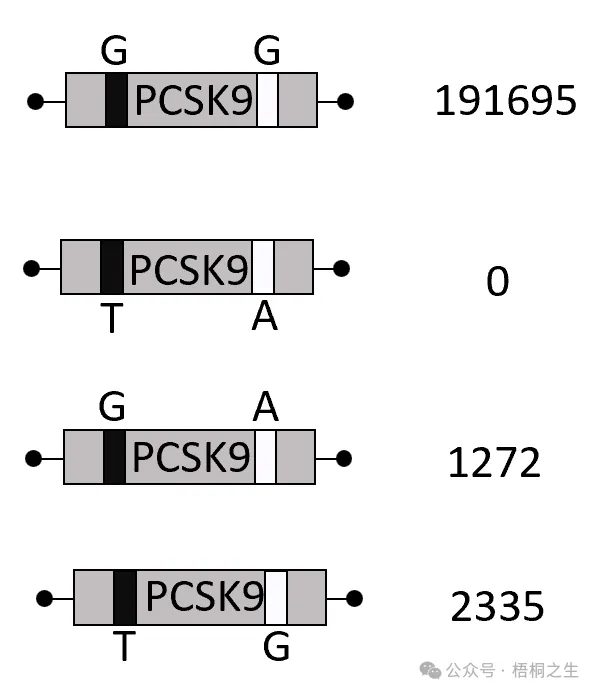
可以看到，最终算法的估算结果是第二种单倍型T-A在人群中的数量=0，换句话说，几乎可以认为人群中不存在顺式变异。只要测序同时检出这对变异，几乎可以认为待测个体一定是携带反式变异的，因此有极高的患病风险。

命题分析

上面的过程看起来很复杂，其实说白了就是干了下面这么一件事：

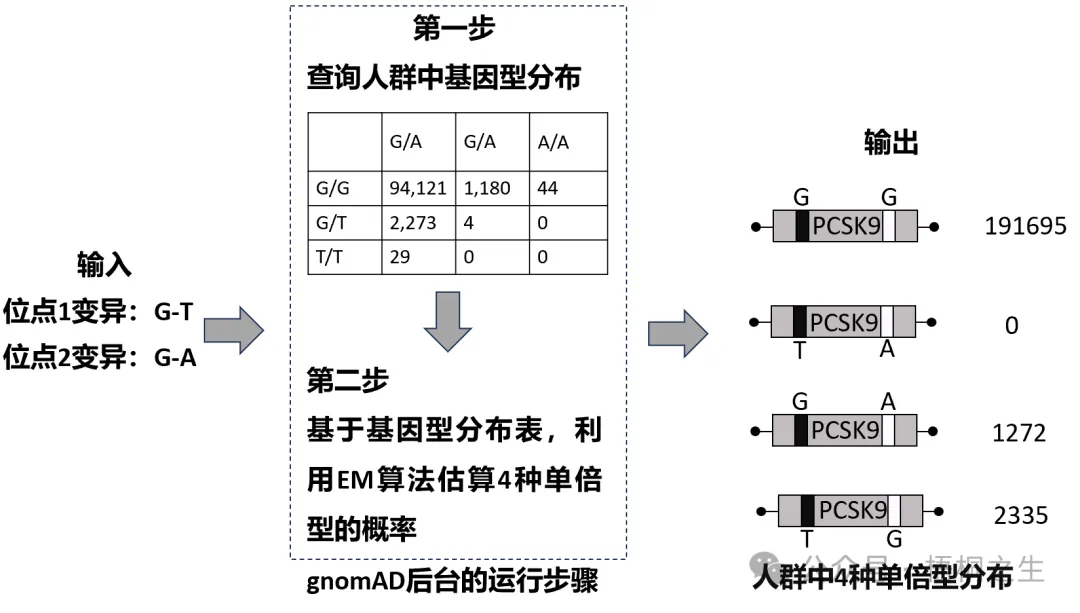
而对临床的医生用户而言，拿到这个单倍型分布后，对手里样本是顺式还是反式的，就大概心中有数了。现在，咱们再看一下原题：

就会发现16题除了B选项涉及到一点对基因型分布表的计算之外，剩余的ACD考的其实是一回事，本质上就是基于人群的基因型分布表，用人脑替代了EM算法，对人群的单倍型分布做了一次定性的估算。而定性分析的背后，运用的统计学中的一条最基本的原理：小概率事件在一次随机试验中通常不会发生。所以，本题中ACD的成立都是基于题干中对该人群的“推测”一词，把推测换成对该人群的“叙述”，这个题就选不出正确答案了。

最后，说点当时看到此题第一眼的感受。能对gnomAD数据库如此了解，我猜应该是一个研究人类群体遗传学的老师命的题。选择呈现一个对高中老师而言几乎都是完全陌生的情境，这题是真没有给那些刷题型、记套路的学生留任何余地，或许只有真正做到灵活运用、融会贯通的学生，才能看穿题目背后的逻辑，从全新的问题里找到解题的关键。

原文链接（梧桐老师已将其保存至网盘）：

链接: https://pan.baidu.com/s/1O_zEHGaX7Di1FauI0feOHw?pwd=drnu 提取码: drnu

来源网址：命题研究 | 还原2025年广东卷16题的命制过程